FLD1_002 קווי זרם, קווי סימון וקווי מסלול

קווי זרם, קווי סימון וקווי מסלול

החלקיק האדום נע בנוזל זורם, קו המסלול שלו מסומן באדום. דיו כחול מוזרק מהראשית וקצה השובל מלווה את החלקיק, אולם בשונה מקו המסלול הסטטי (אשר מתעד את התנועה הקודמת של החלקיק), דיו אשר מוזרק לאחר שהנקודה האדומה מתנתקת ממשיך לנוע מעלה עם הזרם (זהו קו סימון). הקווים המקווקוים מתארים את שדה מהירות הזורם (קווי זרם) אשר מראים את תנועת הזורם באותו הזמן. (“קווי זרם, קווי סימון וקווי מסלול,” 2024).

קווי זרם

קווי זרימה הם קווים המשורטטים על שדה הזרימה כך שבכל נקודה הם משיקים לכיוון הזרימה. מאחר והקווי זרימה משיקים לוקטור המהירות בכל נקודה, לא תיתכן זרימה לרוחב הקו (למשל, במאונך אליו).

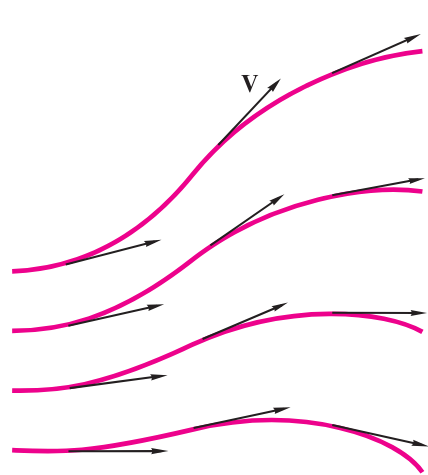
קווי זרימה משיקים בכל מקום לוקטור המהירות (White & Xue, 2021)

כיוון שקווי הזרימה משיקים לוקטור המהירות בכל נקודה, עבור זרימה דו-ממדית אנו יכולים לרשום:

נוכל לפתח הגדרה יותר רשמית ע”י הגדרת פונקציית זרם . נוכל לייצג שני רכיבים - רכיבי המהירות של זרימה דו-ממדית פונקציה אחת .

הגדרה:

פונקציית זרם בדו-ממד מוגדרת בצורה הבאה:

קו מסלול

קו מסלול/קו חלקיק הוא המסלול של חלקיק זורם מסוים מרגע ועד לזמן . כדי לראות קווי מסלול, אנו יכולים לסמן חלקיק ע”י עשן או דיו, ואז לעקוב אחריו.

קו מסלול הוא למעשה תיאור לגראנז’י, והוא למעשה עקומה במרחב התלויה בפרמטר :

משדה המהירות, אנו יכולים לחלץ אותו עבור כל נקודה כללית , בעזרת מערכת המד”ר הבאה:

קו סימון

לפעמים נרצה להתמקד במיקום קבוע מסוים, ולמדוד מה קורה לנוזל שעבר בנקודה זו. למשל, אם נסמן את הנקודה בדיו, לאחר זמן מסוים מספיק חלקיקים יעברו בנקודה, כך שנוכל לזהות את התנהגות הזורם לאחר הנקודה המסומנת. הקו שמחבר בין החלקיקים האלו נקרא קו סימון.

קווי סימון של נקודה מסוימת על כנף.

חשוב להבחין שקו סימון נותן לי עבור זמן מסוים עקומה המתארת את מיקום החלקיקים מ- עד ל- - בשונה מקו מסלול, שנותן לי את המסלול עצמו שעבר חלקיק כלשהו מזמן ועד לזמן .

כדי למצוא את קו הסימון, נעזר בעקומת קו מסלול. בעזרתה, נרצה למצוא בעזרתה, עבור כל , את מיקום החלקיק שיצא בזמן מ-, כעת, בזמן .

תרגילים

שאלה 1

נתון שדה מהירות תמידי, דו-ממדי: כאשר קבוע חיובי.

סעיף א’

הראו כי קווי זרם עבור שדה זה הינם מסוג .
פתרון:
בדו-ממד, אנו יודעים לומר שעבור פונקציית הזרם:

נציב את שדה המהירות:

קיבלנו שפונקציית הזרימה שלנו היא מהצורה:

סעיף ב’

כתבו ביטוי עבור התאוצה בשדה זרימה זה.
פתרון:
במערכת קרטזית, אנו יודעים ש:

עבור כל רכיב בנפרד:

ולכן:

סעיף ג’

כתבו ביטוי עבור מיקום החלקיקים כפונקציה של הזמן, מהצורה:

כאשר בזמן החלקיק היה ב-.
פתרון:
נרשום את משוואת התנועה של החלקיק:

נציב את תנאי ההתחלה שלנו ונקבל:

סעיף ד’

חשבו את התאוצה תוך שימוש בסעיף ג’ והשווה עם התוצאה מסעיף ב’.
פתרון:
נגזור פעמיים לפי :

נשים לב לתוצאה בסעיף ג’, ונקבל:

שאלה 2

ברגע , חלקיקים מתחילים לצאת באופן רציף ממרכז ארובה (באיור נתון מבט מלמעלה), כאשר בחוץ נושבת רוח קבועה בכיוון :

מי מהתיאורים נכון בזמן ?

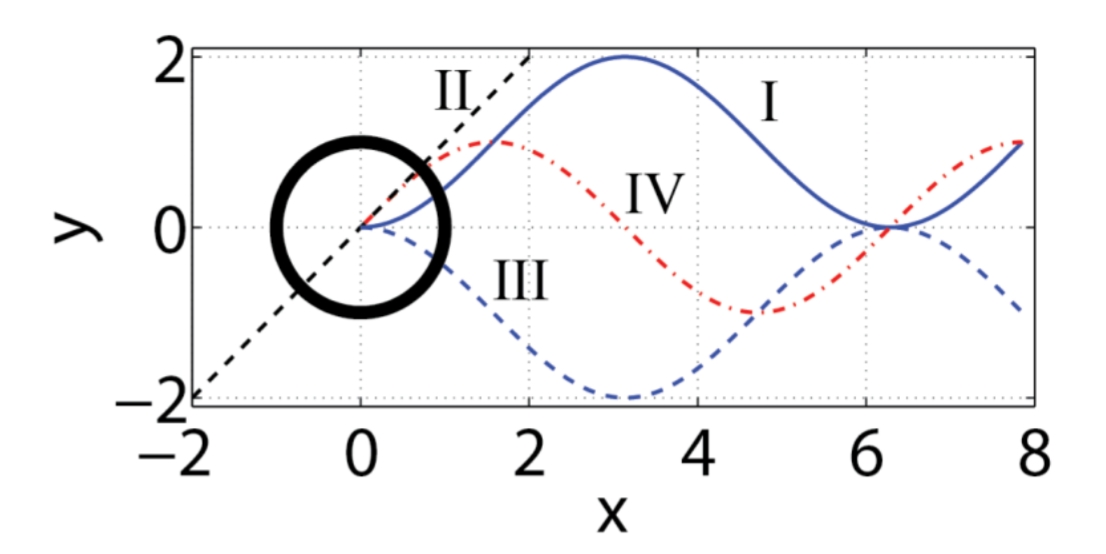
מבט מלמעלה למערכת הנתונה.

פתרון:
שדה המהירות שלנו הוא:

ניתן לראות משדה המהירות שב-, לחלקיק אין מהירות בכיוון , אלא רק בכיוון . בנוסף, עבור , ערך המהירות בכיוון הוא חיובי, כך שהחלקיק ינוע גם בכיוון החיובי של . לכן, קו הוא קו מסלול/חלקיק. מבחינה מתמטית, בהתחלה:

משדה המהירות:

מהצבת תנאי ההתחלה נקבל:

שזהו אכן קו .

ברגע , שדה המהירות שלנו:

קווי הזרם משיקים לשדה המהירות בכל נקודה, ולכן הוא קו הזרם ב- . מבחינה מתמטית, מהגדרת קווי זרם:

נציב משדה המהירות:

ברגע :

קו אכן ניתן לתיאור ע”י פונקציה זו.

אנו יודעים שברגע האחרון, , החלקיק שיצא ב- מהראשית הוא בעצם חלק מהקו סימון ב- . הקו היחיד שפוגש את חלקיק זה (הנקודה האחרונה בקו המסלול) הוא קו , ולכן הוא קו סימון. מבחינה מתמטית, אנו יודעים שהמיקום:

נסמן פרמטר רץ , שבעזרתו נוכל לדעת איפה חלקיק היצא ברגע מהנקודה נמצא ברגע .

נציב בחזרה במיקום:

ברגע :

שזהו אכן קו .