DYN1_HW002 תרגיל בית 2

תרגיל 1

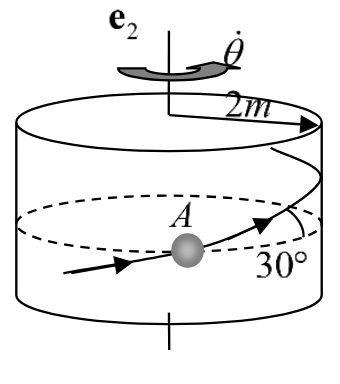
נתונים:

סעיף א’

נעבוד במערכת צירים גלילית - .

התאוצה הכללית היא:

הגודל הוא קבוע ולכן:

נציב בנתון על התאוצה המשיקית:

גודל התאוצה נתון ע”י:

סעיף ב’

המהירות במערכת קואורדינטות גלילית נתונה ע”י:

הגודל קבוע. בנוסף, כבר מצאנו את בסעיף קודם:

אנו יודעים את המהירות הזוויתית ואת רדיוס המסלול , ואת זווית המסלול של החלקיק. כלומר, המהירות האנכית של החלקיק מוגדרת היטב לפי הגאומטריה:

נציב:

סעיף ג’

גודל התאוצה נתון ע”י:

תרגיל 2

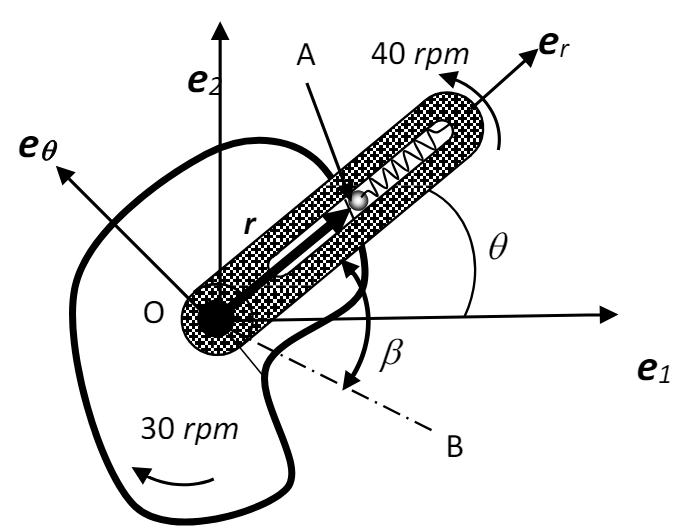
סעיף א’

תאוצת הכדור בקואורדינטות פולאריות:

במקרה שלנו, , כך שמתקיים גם .
הפיקה עומדת, כך ש- נשאר בתנאי התחלה שלו, ולכן מתקיים בכל רגע. לכן נוכל לומר כי גם:

בנוסף, נשים לב כי:

נציב בביטוי לתאוצת הכדור:

נציב נתונים וערכים שמצאנו:

סעיף ב’

כעת המוט עומד והפיקה מסתובבת, כך ש- בכל רגע נתון ולכן גם . עבור :

הנגזרות של מסעיף קודם עדיין נכונות עבור סעיף זה. נציב בביטוי לתאוצת הכדור:

נציב נתונים וערכים שמצאנו:

סעיף ג’

המוט מסתובב נגד כיוון השעון:

הפיקה מסתובבת בכיוון השעון. נמדדת בין המוט המחורץ (שמסתובב) לבין הקו (שמסתובב). לכן:

נציב בביטוי לתאוצת הכדור:

נציב נתונים וערכים שמצאנו:

תרגיל 3

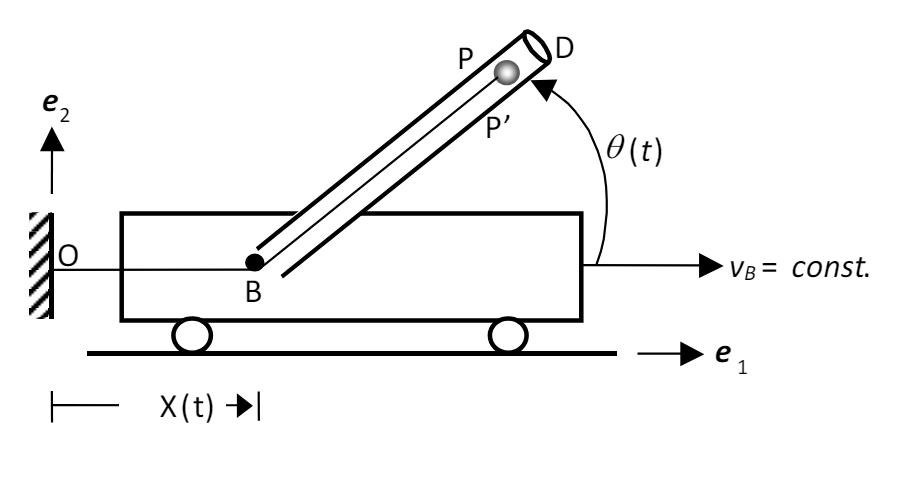
תיאור הבעיה.

סעיף א’

מערכת הצירים הפולארית בה נשתמש.

סעיף ב’

מהירות החלקיק ביחס ל- במערכת הצירים הפולארית:

מגיאומטריית המבנה:

נציב במהירות היחסית:

המהירות המוחלטת:

נשים לב כי:

נציב במהירות המוחלטת:

סעיף ג’

תאוצת החלקיק ביחס ל-:

נציב את הנגזרות של מסעיף קודם:

התאוצה המוחלטת:

התאוצה היא אפסית כי קבוע. לכן:

סעיף ד’

הצינור והחלקיק מסתובבים יחד, כך שהמהירות המשיקית שלהם זהה. לכן, יחסית לצינור, המהירות המשיקית של היא אפס, ונשארת רק המהירות הרדיאלית:

סעיף ה’

גודל המהירות: