| סטודנט א’ | סטודנט ב’ | |
|---|---|---|
| שם | עידו פנג בנטוב | ניר קרל |
| ת”ז | 322869140 | 322437203 |
| דואר אלקטרוני | ido.fang@campus.technion.ac.il | nir.karl@campus.technion.ac.il |
תרגיל 1
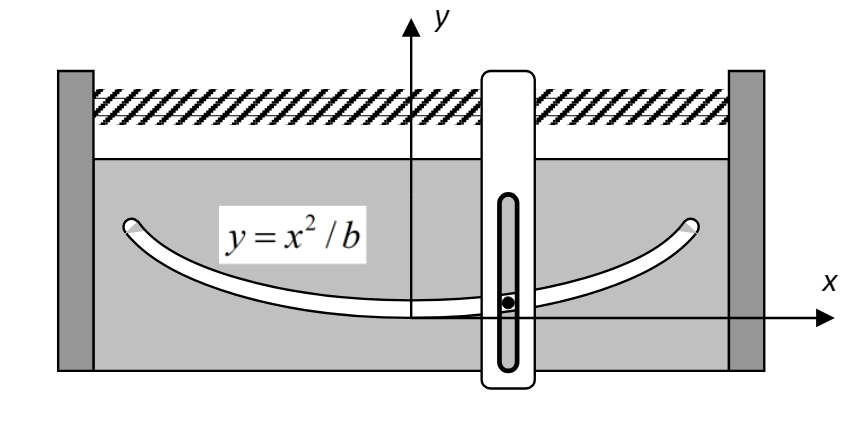
נתון:
סעיף א’
מיקום הפין מאולץ ע”י:
נגזור לפי
ולכן:
סעיף ב’
נגזור את
ולכן:
סעיף ג’
נציב פשוט
תרגיל 2
סעיף א’
נבצע אינטגרציה:
נציב את התנאי התחלה
סעיף ב’
תרגיל 3
סעיף א’
נמצא את
נציב בוקטור המיקום:
ולכן:
סעיף ב’
נמצא עבור איזה
נקבל את המינימום כאשר הביטוי בתוך השורש הוא מינימלי:
נאפס ונגלה כי עבור
סעיף ג’
מסעיף קודם:
סעיף ד’
מסעיף א’ אנו יודעים ש-
תרגיל 4
נתונים:
נוכל לפתור את הבעיה אם נתעלם לגמרי מהזמן
נשים לב כי:
נציב בביטוי הנתון עבור
עבור מקטע כללי:
נציב את הנתונים עבור המקטע הראשון ועבור המקטע השני כדי לקבל את מערכת המשוואות:
נשווה בין שתי המשוואות ונקבל:
נציב במשוואה הראשונה:
-\dfrac{1}{2{c}{2}}\ln({c}{1}+{c}{2}v^{2})\bigg|{{v}{i}}^{{v}{f}} =x\bigg|{{x}{i}}^{{x}_{f}}
\begin{gathered}
-\dfrac{1}{2{c}{2}}\ln({c}{1}+{c}{2}v^{2})\bigg|{16.\bar{6}}^{0}=x\bigg|{0}^{x{f}} \[1ex]
-\dfrac{1}{2{c}{2}}\ln({c}{1})+\dfrac{1}{2{c}{2}}\ln({c}{1}+22.\bar{2}^{2}{c}{2})=x{f}
\end{gathered}
\boxed {
x_{f}=\pu{532.84m}
}